NOTE: This post was originally published on March 18, 2012. It has been updated many times:
2015 to reflect some new findings,
Sep 2016 to include the numerous new hyperbolic features,
Oct 2018 with even more features and links.
The main goal of the HyperRogue project is to see how hyperbolic geometry can be used to achieve great game design (and it succeeds in this goal -- see
e.g. this review on Rock Paper Shotgun).
(This is not the only goal, though -- HyperRogue is probably the most feature-rich engine for non-Euclidean geometry, that can be used for a plethora of visualization, research, and educational purposes; see
RogueViz.)
The purpose of this article is to explain what's the deal.
It is intended for mathematicians interested in hyperbolic geometry who would like a summary of HyperRogue, and for roguelike players who would like to know what hyperbolic geometry is -- some of them think that
HyperRogue takes place on a 3D sphere, or that you will return to the same location if you move in a particular direction for a long time, which is not accurate at all, so I explain it here in more detail.
HyperRogue is a
roguelike computer game. Roguelikes are a genre of computer games that have evolved separately from the mainstream -- even though they are commonly viewed as a subgenre of RPGs, they are in many senses closer to board games, like Chess where you have just one piece and the "chessboard" is randomly generated by the computer, than to other computer games. (Recently the elements of roguelikes, such as procedural generation and the challenge of
permadeath, are added to more and more computer games which do not really have much in common with true roguelikes, causing even more confusion.) In case of HyperRogue, the "chessboard" is an infinite hyperbolic plane. You can read more about it on
Wikipedia. This is not a sphere, but rather a hyperboloid (but also not in a normal space). The 3D object you see when you activate the "eye distance" option is this hyperboloid.
Hyperbolic geometry seems to be underused in art. M.C. Escher has been using it in some of his work (like
Circle Limit). I have seen
Maze, Pool, and Sudoku on a hyperbolic plane, but here the map is looped, and thus IMO less interesting than the real infinite world of HyperRogue. The original concept of Hyperbolic Rogue got quite popular despite being an extremely simple game, so I think this is a great area to explore.
Normally the game presents the world in the so called Poincaré disc model (also used by the art mentioned above). The closer you are to the edge of the disc, the bigger distances are (five pixels close to the edge is a much bigger distance than five pixels in the center). On the Euclidean plane, the boundary of a circle of radius
r is linear in
r. On the hyperbolic plane it is exponential. This means that it is very hard to return to a place where you have already been in HyperRogue. You would have to return almost the same way.
Triangles in hyperbolic geometry have angles which sum to less than 180 degrees. For example, if you take two hexagons and one heptagons next to each other on the HyperRogue map, and construct a triangle with vertices in centers of these cells, the sum is (360/6) + (360/6) + (360/7) = 171.4 degrees, so there is a "defect" of 60/7 = 8.6 degrees. The defect is proportional to the area of the triangle. (Similar thing happens on a sphere: a triangle with a vertex on a pole and two on the equator has 90+90+90 = 180+90 degrees, which is π/2 more than 180 degrees, and the total area of the sphere is 4π, which corresponds to eight of our triangles.) The visible in-game effect of this is that if you go from A to B, from B to C and from C back to A, the screen will (probably) appear rotated, making it easier to get lost.
This is the map structure I have found most suitable for a roguelike (or other similar grid-based game). Three hexagons would sum up to 180 degrees and we would get a plane. Three heptagons in each corner would be possible, but they would be too big (each of them would take the space of one heptagon in HyperRogue plus 1/3 of each hexagon surrounding it).
Now how does this relate to the actual gameplay? As already mentioned, an important result of using the hyperbolic plane is that you almost never get into a place where you have been before. Some of the areas make other aspects of the hyperbolic geometry important, and some are just for fun.
 Land of Eternal Motion::
Land of Eternal Motion::When you are running away from monsters on a straight line in the Land of Eternal Motion, monsters cannot follow you on the same line, they have to use an equidistant curve instead. Since these curves are longer in hyperbolic geometry, it is quite easy to run away.
 Hunting Grounds::
Hunting Grounds::
In lands other than Land of Eternal Motion, when you are running away from a monster, it will have to chase you on exactly the same path as you, and if there are several monsters, they will have to make a queue. In most roguelikes, the basic strategy is that, when attacked by a group of monsters, you should run into a corridor, and fight them one by one. In HyperRogue, this effect can be achieved in an empty space.
At low treasure counts, Hunting Grounds pits you against several dogs. Use the effect above to queue them up -- that would not be possible in an Euclidean hex grid (where they would pursue you forever), or in a spherical tesselation (where three dogs would eventually get you).
At higher treasure counts you also get ambushed by dogs, apparently from "all" directions. However, in the hyperbolic plane, there are more directions than it appears, so you can still escape!
 Crossroads (and walls in general):
Crossroads (and walls in general): walls separating different areas are straight lines, and they do not cross. You cannot have that many non-crossing straight lines in a Euclidean world.
 Land of Mirrors:
Land of Mirrors: mirages would be very nice to play in a Euclidean world (see
DROD's mimics for something very similar), my point here was to check how this would work in a hyperbolic plane. The result seems to be that they are mostly annoying (they are supposed to stay parallel to you, but parallel lines diverge too quickly).
In later versions, the Land of Mirrors has been replaced with
Hall of Mirrors -- this adds mirrored walls that the Mimics can reflect off; this makes the land interesting in hyperbolic plane too :)
 Living Caves:
Living Caves: the cave has a tree-like structure: you go into a tunnel, sometimes you find forks, and you can be almost sure that both of the new tunnels do not end, and in fact, they quickly fork again. And loops are extremely unlikely. In an Euclidean world, this would not work. It would be at least a bit different.
 Alchemist's Lab:
Alchemist's Lab: a bit like the Living Caves, the hyperbolic nature of the map means that you can usually get as far as you want in roughly any direction, no matter whether what color you are on. From the game
Hex we know that, in Euclidean geometry, if there is a red connection between top and bottom the screen, there is no blue connection between left and right. While this is still true in hyperbolic geometry, it does not feel like that, because we have many more directions there. This has ties to
the percolation theory.
 Icy Lands:
Icy Lands: that's a minor difference, but heat disperses more quickly here than it would on a Euclidean plane (actually the model in the original tech demo was a bit wrong).
 Camelot:
Camelot: In Camelot, you have to find the Holy Grail, which is in the center of the Round Table. The Round Table is a circle of radius 28. The number of cells in a circle of radius r is roughly 3 to the power of r/2; in particular, there are 31659398 floor tiles inside the table, and 22860754 tiles of the table. Thus, when you start on the table and start moving in a completely random direction, you will run straight into the Holy Grail with probability only 1/31659398 -- if you choose the direction based on the shape of the table, the probability is of course higher, but still, after a small number of steps you will usually end up back at the Table. You need to invent some strategy to precisely take you to the center.

The
Hive is an attempt at depicting how a war in hyperbolic plane would look. In our world, an army has a first long row of soldiers, then the second row, and so on. This way, the army moves quickly, and many soldiers can fight in parallel. However, this does not work in the world of HyperRogue: one column of soldiers may move on the straight line between points A and B is the shortest route, but if we have another column, it will have to move on an equidistant curve, which will be much longer. Therefore, if the army wants to move quickly, it will have just a small number of columns.
 Horocycles:
Horocycles: In the Hive and Camelot, you could see how big circles look in the hyperbolic plane. While in the Euclidean world, big circles resemble straight lines more and more, the situation in the world of HyperRogue is different -- they always look curved. If you are standing on a circle, it is easy to tell that this is not a straight line -- but locally, a fragment of a circle of radius, say, 10 tiles will look almost exactly the same as a fragment of a circle of radius, say, 100 tiles. A horocycle is what we get in the limit -- something like a circle of infinite radius. The
Temple of Cthulhu is an infinite sequence of horocycles, where you have to go deeper and deeper to get more points, and
Whirlpool is a
horocycle which draws you toward its infinitely distant center.
 Caribbean
Caribbean is unmarked, and shows that, just as in Camelot, it may be hard to find the direction towards the center of the horocycle -- you have to use compasses to lead you there.
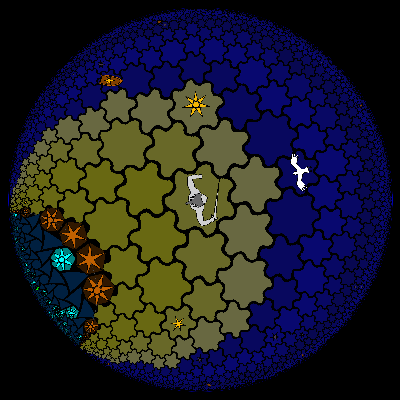
A Great Wall is a straight line, and the coast is an equidistant curve at some distance from this great wall (the distance changes with the tides). As you can see, it is hard to tell the difference between a large circle, horocycle, or a distant equidistant -- so if you are in the Ocean, it is not immediate to tell whether the waves you see are because of the nearby coast, or because of the nearby Whirlpool. See
this article by Fulgur14 to read more about circles, horocycles, and equidistant curves.

The
Haunted Woods is a land from where there is just one exit -- it is bounded by a single curve. For further confusion, this curve may look like a circle or horocycle, but it is not -- it is an equidistant curve -- while moving randomly inside a horocycle quickly gets you to its edge, in the Haunted Woods, if you cross the straight line and go randomly on the other side, you will likely be lost forever in the Haunted Woods, as you have to return to the location where you have been before, and this is virtually impossible, due to the exponential growth. The
Yendor Quest is based on the same principle -- you have to go 100 steps to find the Key, then return. There is a marker which shows your way to the Key, but you have to return on your own, which is virtually impossible based only on luck or memory.

In the
Princess Challenge, a mouse asks you to reach the Princess, locked somewhere in the Palace. She is 100 steps away, so you would not find here without help -- luckily, the mouse will lead you. The screenshot above shots the cell where the Princess is locked -- you have to press the green button in bottom left to open the doors; when you first see the princess, you are typically on the other side, and have to go around all these closed doors. This exhibits interesting properties of hyperbolic mazes -- there are obstacles on the way, and sometimes you will have to do significant detours to go around them, but if you know what you are doing, you will eventually reach the Princess with probability of (almost) 1. This is related to
branching processes.

The
Crossroads III, as well as
the Elemental Planes later in the game, show straight lines which cross at straight angles.

The
Ivory Tower shows you how gravity could work in the hyperbolic world. Gravity is directed towards a straight line, thus making the horizontal levels into equidistant curves. Interestingly, while in the most of the game it is very hard to return to the location you have been to, in these lands, you simply go with the gravity to exit, and you turn up at almost exactly the same location you started. This is because, as usual, levels grow exponentially: moving 243 cells on the level 20 corresponds to moving just 243/3
(20-10)/2 = 1 cell on level 10.

The
Yendorian Forest is another land in gravity. We already had straight lines that cross, and that are ultraparallel (diverging). Branches of the same tree in the Yendorian Forest are straight lines that diverge when you go upwards, but get closer and closer when you go towards the base level.

There are regular patterns in Euclidean plane, which generally look like grids. We also have regular patterns in the hyperbolic plane, but they look more like infinite trees. Such regular patterns appear in the
Vineyard,
Land of Power,
Zebra,
Windy Plains,
Emerald Mine, and
Palace. The picture above shows the Vineyard; see the
Gallery of Lands for the screenshots of the remaining regular lands.

In the
Burial Grounds, you have to fight enemies and excavate treasures, using a magical energy sword. This sword stays at the same relative angle to you when you move. However, after you go in a closed loop, the sword will usually be rotated, because of how angles work in the hyperbolic plane! This land obviously makes no sense in the Euclidean mode.

In
Galápagos, each tortoise has 21 binary properties, thus leading to 2
21 = 2097152 subspecies. Tortoises at the given spot are usually exactly the same, but as you travel, the environmental properties change smoothly, and so do the properties of Tortoises. You have found a (random) baby tortoise, and you have to find a tortoise which exactly matches the baby. This would not be feasible in the Euclidean plane -- even if you exactly knew where the correct tortoise are, you would still have to go 1000 steps to reach it, but since you don't know, you would have to wander blindly. In the hyperbolic plane, the correct tortoise is always actually quite close, because of the exponential growth; furthermore, the simple method of always going towards the direction where more properties agree works. The coloring of tiles in the Galapagos (based on the number of factors which agree), as well as the height function used to generate the
Dragon Chasms, is related to a generalization of
the Wiener process to the hyperbolic plane domain -- there are similar generalizations to
Euclidean plane domains, but for hyperbolic plane this is mathematically much more elegant.

You can also change the geometry in HyperRogue. The first alternate geometry was, of course, the Euclidean mode -- see
this old post about it. In 2018 the big part of work on HyperRogue was adding more and more geometries to experiment with. Disable bitruncation for stronger hyperbolic effects; apply the Goldberg-Coxeter construction to weaken them (which may make you lose to dogs in LoEM or Hunting Grounds -- even though the world is globally hyperbolic, there are parts which are flat); play on the sphere; use irregular, or mostly arbitrary Archimedean tilings; and so on. See
this article for all the possibilities.
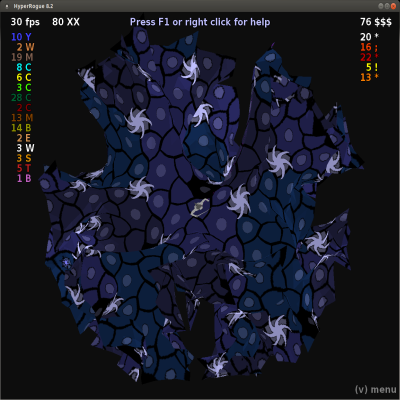
The Poincaré disc model is just one of many possible models ("maps") that can be used to display the hyperbolic plane. HyperRogue also lets the players to play with other models. In the band model, you can see that your route through the game is almost a straight line; in the half-plane model, horocycles are horizontal and branches of Yendorian Forest are (almost) vertical; in the Klein model, straight lines look straight; the Hypersian rug model lets you play on something similar to the
hyperbolic crochet, and the paper model creator even lets you to print it. See
this article for more details.